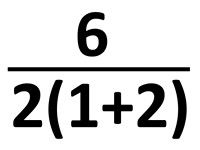数式の曖昧さを回避することを考えておかないと計算結果がまったく違うことになる可能性があります

2024.05.07
この記事は約4分で読めます。

数式の曖昧さを回避数式の解釈には曖昧さがあるということがわかりました。例えば、この画像のように分数で表示すると計算結果は「１」になりますが、数式で表示した場合の計算結果は「９」になる場合があるということです。
それが数式の曖昧さということですが、正しい計算順序が一部不明確ということのようです。どういうことかということを備忘録として載せておきます。

数式には曖昧さがあります

分数にすると計算しやすいです

計算式では、まず分数にして計算するという方もいると思います。

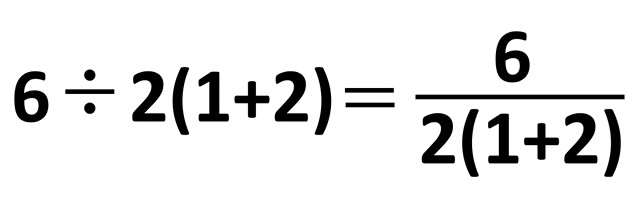
上記の式で、左辺と右辺が同じであれば、右辺の分数のほうで計算をすることができます。
分数にすれば、計算順序は明確になります。

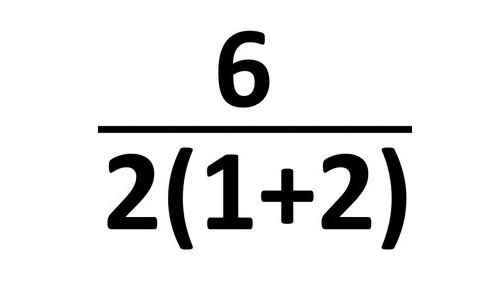
分母の方を計算すると、２×（１＋２）＝２×３＝６となります。
分子は６ですから、分数で6/6＝１ですね。

数式 6÷2(1+2) の計算結果は？

あらためて、この数式の計算をしてみてください。


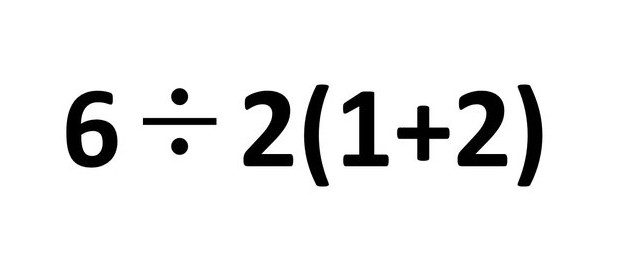
この数式を計算する際には、四則演算の順序である「かっこ」「乗除」「加減」の順に計算を進めます。具体的に計算ステップは以下の通りです。

  1. まず、かっこ内の計算を行います。
    1+2=3
  2. 次に、乗除の計算を進めます。式が 6÷2×3 となります。
    ここで注意が必要ですが、乗除は左から右への順番で計算されるため、まず 6÷2 を計算します。
    6÷2=3
  3. 最後に、残りの乗算を行います。
    3×3=9

よって、この式の答えは 9 です。

数式の計算結果が２種類、どっちが正しいのでしょうか？

まったく同じ数式のはずなのに、計算結果が１の場合と９の場合がでてきてしまいました。これは困ります。

どちらが正しいのでしょうか？

あらためて調べてみると、「どちらの計算結果もありうる」ということでした。

え、それはおかしいでしょ、と思いますよね。数式の解釈が違うことで計算結果が違うということです。

この現象についてさらに調べてみました。

この不思議な現象をChatGPTに説明してもらいました

どもども遠田
どもども遠田

四則演算を正しく実施した場合の 6÷2(1+2)=9 という計算結果と、分数にしてから計算した場合の1とは回答が矛盾しますね。
あらためて説明してください。

この質問に対するChatGPTの回答は以下のとおりでした。

どもども遠田
どもども遠田

このような数式の曖昧さを回避するためには、どうすればいいですか？
たとえば、割り算のところは分数を使うことで曖昧さは回避できますか？

AIの回答
AIの回答

数式の曖昧さを回避するためには、より明確な表記方法を用いることが重要です。特に、割り算や乗算を含む式では、どの操作が先に行われるべきかを明確にすることが必要です。以下に具体的な方法をいくつか示します。

 

分数表記の使用

割り算を示す場合、特に複数の項が関わる場合は、分数の形式を用いると明確になります。
例えば、 6÷2(1+2) という式を

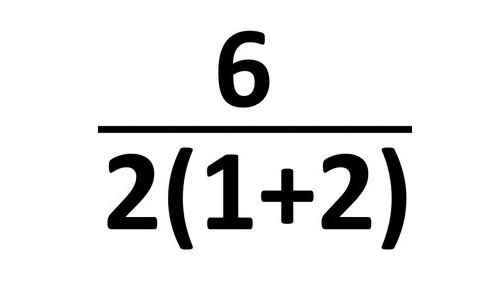
と表記することで、分母の全体がまず計算されることが明確に示され、解釈の曖昧さが減少します。

括弧の利用

演算の順序を明確にするために括弧を使うことも有効です。例えば、乗算を割算の前に行いたい場合、括弧を使って 6÷(2×(1+2))と表記することができます。これにより、どの部分を先に計算すべきかが明確になります。

明確な演算子の使用

特にプログラミングや一部の数学の文脈では、割り算を示すためにスラッシュ（/）の代わりに分数バーを使用するとより明確です。また、乗算記号としてアスタリスク（*）を使用することも、乗算を明示的に示す手段として有効です。

 

文書や指示での補足説明

教科書や試験、指示書などでは、数式の意図を文章で補足することで、どのように計算すべきかを明確にすることができます。

 

これらの方法を適切に使用することで、数式の曖昧さを減らし、誤解を避けることができます。

今回の数式は単純なもので目視できましたので、確認や修正もできそうです。

しかし、実際にシステムで使う数式だとそのような曖昧さが残ってはいけません。システムを作るのは人間ですから、人間同士の段階で勘違いが起きないように注意したいですね。